Cvičenie 3: ARMA procesy
Príklad 1
Uvažujme časový rad \(x_t = -2t + u_{t} + 0.5u_{t-1}\), kde \(u_t \sim N(0,\sigma^2) \) je biely šum.
- Nájdite strednú hodnotu a autokovariančnú funkciu časového radu \(x_t\).
- Je daný časový rad stacionárny? Zdôvodnite.
Príklad 2
Uvažujme časový rad, ktorý predstavuje prvé diferencie časového radu z Príkladu 1, t. j. \( y_t = \Delta x_t = x_t - x_{t-1} \)
- Nájdite strednú hodnotu a autokovariančnú funkciu časového radu \(y_t\).
- Je daný časový rad stacionárny? Zdôvodnite.
Príklad 3
Uvažujme realizácie dvoch rôznych stacionárnych časových radov \(x_1, x_2, x_3, ..., x_T \) a \(y_1, y_2, y_3, ..., y_T \). Na obrázku nižšie sú zobrazené ich výberové autokorelačné funkcie a výberové parciálne autokorelačné funkcie. Ako by ste dané časové rady modelovali? Použili by ste AR(p) alebo MA(q)? Aký rád by ste zvolili? Zdôvodnite.
-
Časový rad \(x_1, x_2, x_3, ..., x_T \):
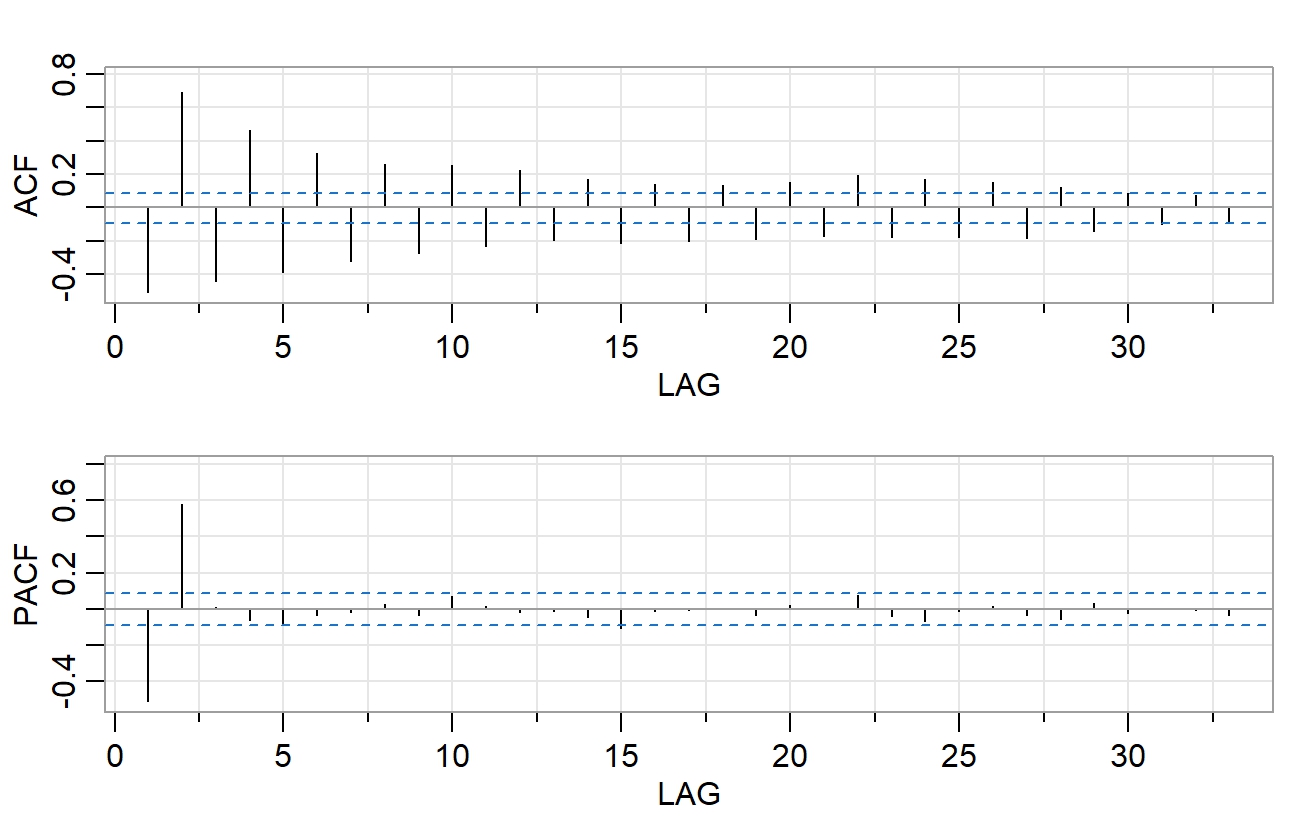
-
Časový rad \(y_1, y_2, y_3, ..., y_T \):
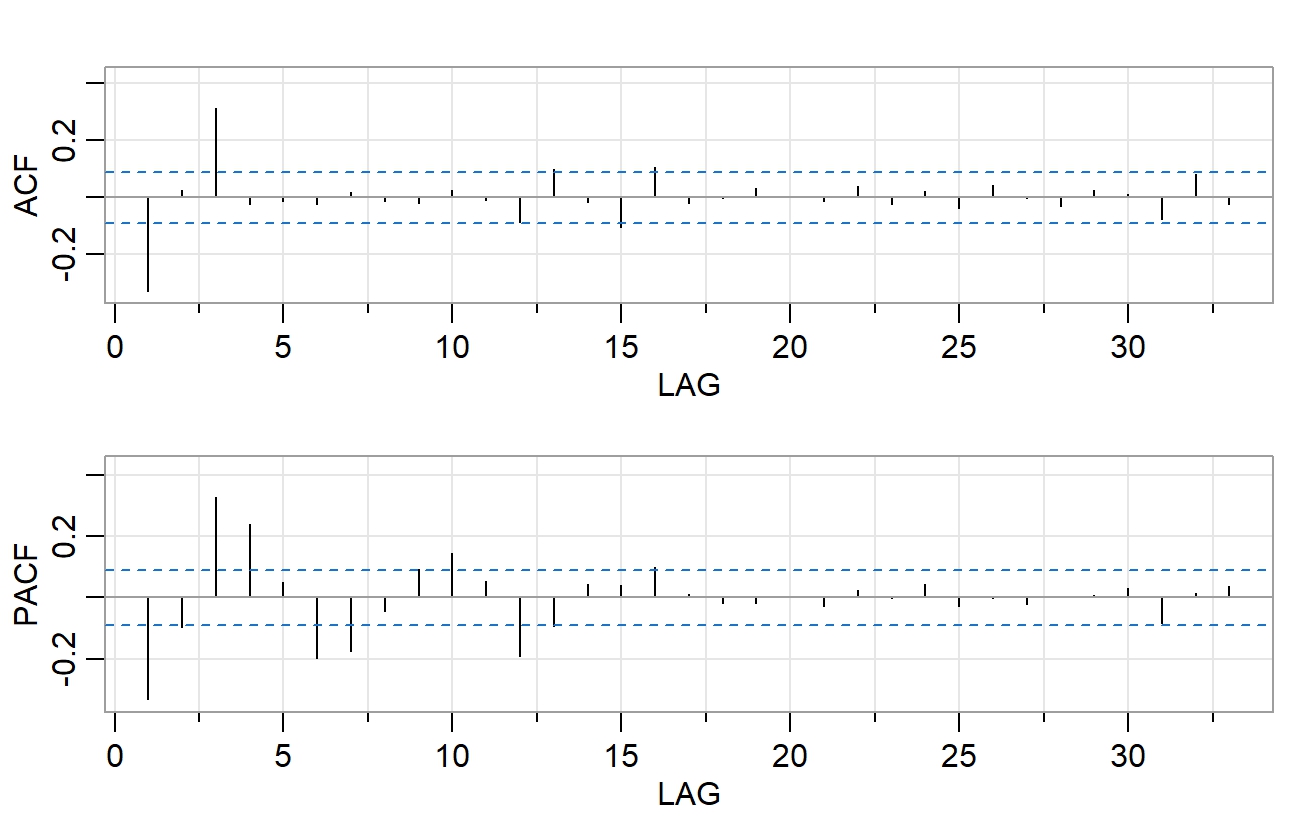
Príklad 4
Uvažujme ARMA proces \( x_t = x_{t-1} - 0.25 x_{t-2} + u_t - 0.25 u_{t-1}\), kde \(u_t \sim N(0,1) \) je biely šum.
- Je daný proces stacionárny? Zdôvodnite.
- Dopočítajte koeficienty \( \psi_j \) z Woldovej reprezentácie daného procesu, \(x_t = \mu + \sum_{j=0}^\infty \psi_j u_{t-j}. \)
Príklad 5
Uvažujme ARMA proces z Príkladu 4, t. j. \( x_t = x_{t-1} - 0.25 x_{t-2} + u_t - 0.25 u_{t-1}\), kde \(u_t \sim N(0,1) \) je biely šum.
- Je daný proces invertovateľný? Zdôvodnite.
- Dopočítajte koeficienty \( \pi_j \) z AR\((\infty)\) reprezentácie daného procesu, \(u_t = x_t + \sum_{j=1}^\infty \pi_j x_{t-j}. \)
Príklad 6
Uvažujme proces \( x_t = \frac{1}{2} x_{t-1} + u_t - \frac{1}{3} u_{t-1}\), kde \(u_t \sim N(0,1) \) je biely šum.
- Odvoďte diferenčnú rovnicu a počiatočné podmienky pre autokovariancie. Rovnicu vyriešte (nájdite explicitný predpis autokovariančnej funkcie).
- Odvoďte diferenčnú rovnicu a počiatočné podmienky pre autokorelácie. Rovnicu vyriešte (nájdite explicitný predpis autokorelačnej funkcie).
Pozn.: Príklady 1, 2, 4, 5 sú prebraté z Midterm testu pre kurz Stat 153: Introduction to Time Series, Fall 2010, UC Berkeley. Zdroj: https://www.stat.berkeley.edu/~bartlett/courses/153-fall2010/hw/mt1.pdf