Cvičenie 3: AR(p) model, stacionarita a Woldova reprezentácia
Výpočty v R-ku z hodiny: mPMS_Cv3_R.html
Príklad 1
Uvažujme proces \(x_t = 5 - 0.4x_{t-1} + 0.1x_{t-2} + u_t\).
- Ukážte, že je proces stacionárny.
- Odvoďte diferenčnú rovnicu a začiatočné podmienky pre koeficienty Woldovej reprezentácie.
- Vypočítajte rekurentne niekoľko prvých členov. Potom odvoďte explicitný predpis pre všeobecný člen.
Príklad 2
Uvažujme proces \(x_t = 5 + 0.4x_{t-1} - 0.1x_{t-2} + u_t\).
- Ukážte, že je proces stacionárny.
- Odvoďte diferenčnú rovnicu a začiatočné podmienky pre koeficienty Woldovej reprezentácie.
- Vypočítajte rekurentne niekoľko prvých členov. Potom odvoďte explicitný predpis pre všeobecný člen.
Príklad 3
Zistite, či sú nasledovné AR procesy stacionárne:
- \( (1 + 0.3L + 0.2L^2)x_t = u_t\)
- \( (1 - 0.25L + 0.6L^2 - 0.55L^3)x_t = u_t\)
- \(x_t = 0.8x_{t-1} + 0.3x_{t-2} + 0.2x_{t-3} + u_t\)
- \(x_t = 0.25 + 0.1x_{t-1} + 0.2x_{t-3} + u_t\)
Príklad 4
Nájdite príklad- Stacionárneho AR(3) procesu
- Nestacionárneho AR(4) procesu
- Stacionárneho AR(2) procesu, ktorého stredná hodnota je rovná 15.
Príklad 5
Vyjadrite podmienku stacionarity pre AR(2) proces v tvare nerovností pre parametre procesu a toto tvrdenie dokážte.
Príklad 6
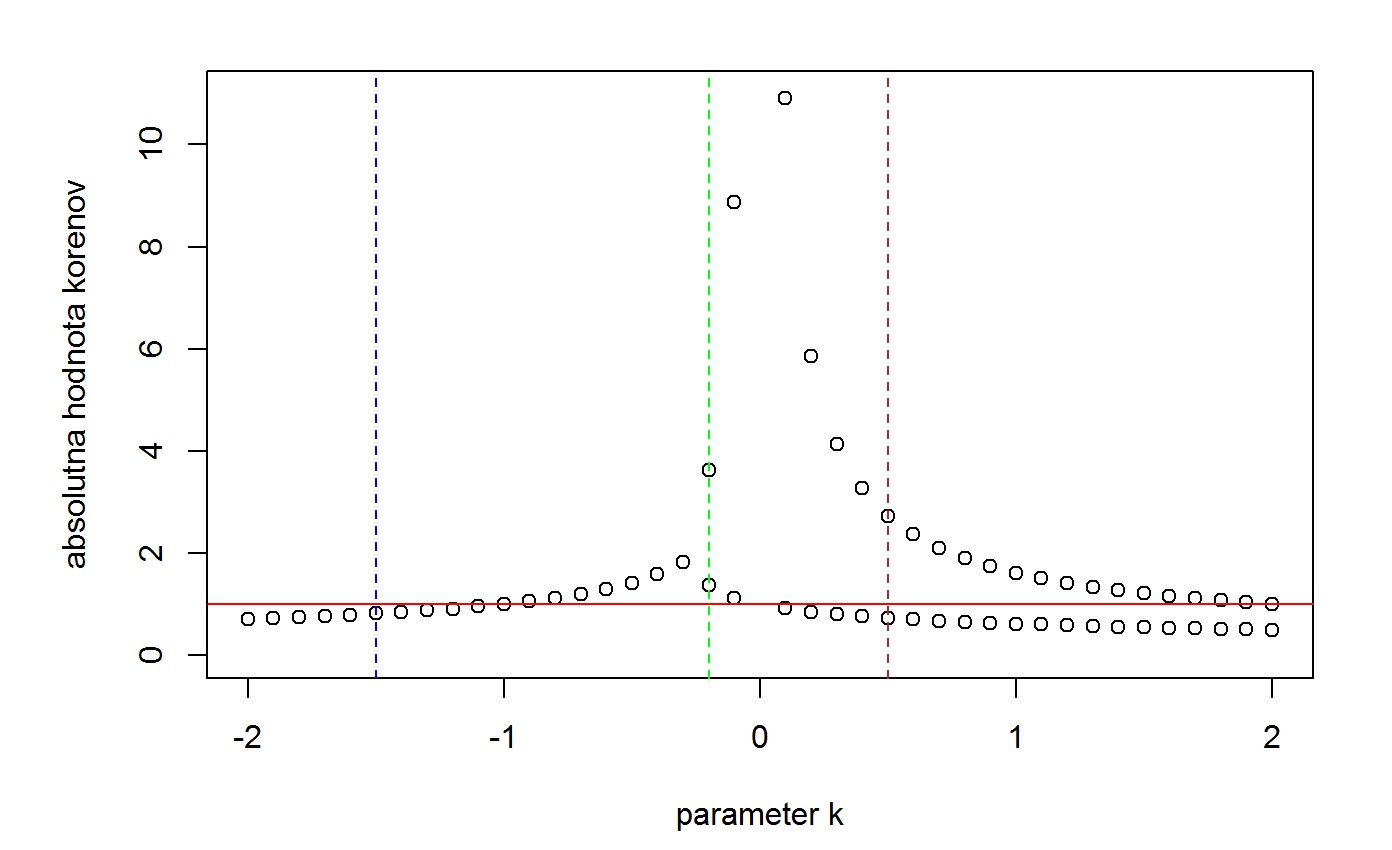
Pre aké hodnoty parametra \(k\) je proces \(x_t = x_{t-1} + kx_{t-2} + u_t\) stacionárny? (môžete využiť podmienku odvodenú v predošlom príklade)
Skontrolujte, či sa vaše výpočty zhodujú s numerickými na nasledujúcom obrázku. Prečo pre niektoré \(k\) je len jedna absolútna hodnota (napríklad \(k= -1.5\) - modrá), kým pre iné sú dve (\(k= -0.2\) - zelená, \(k= 0.5\) - hnedá)?